

TRANSMISSIVITY DISTRIBUTION IN THE TUCSON BASIN AQUIFER
Donald J. Supkow, Ph.D.
Ed. By: William M. Turner, Ph.D.
INTRODUCTION
This study is an outgrowth of an effort by the University of Arizona, Department of Hydrology and Water Resources to construct a digital model of the Tucson Basin aquifer. Of particular importance in the construction of digital and electric analog models of non-homogeneous aquifers is the spatial distribution of aquifer transmissivity.
A casual inspection of the areal distribution of aquifer transmissivity within the Tucson Basin aquifer as determined by aquifer-performance tests (University of Arizona Agricultural Engineering files) and as reported by Anderson (1970) indicates that the values of transmissivity are not randomly distributed in space.
Low values of aquifer transmissivity (<5,000 gallons per day per foot (<62 m2/d) occur around the periphery of the basin whereas larger values of aquifer transmissivity (greater than 100,000 gpd/ft (1,240 m2/d) occur within the central and outlet parts of the basin. This is manifested by a general trend of increasing aquifer transmissivity in the direction of ground-water flow.
Gates (1972) found the frequency distribution of aquifer transmissivity in the Tucson Basin, as determined by aquifer-performance tests, to be normal or log-normal. Such a sample is biased in that people tend to drill wells in known areas of high transmissivity and avoid drilling wells in areas of known low transmissivity. The frequency distribution of transmissivity as derived from a calibrated and validated digital computer model of the Tucson Basin aquifer is thought to be more nearly representative of the real world because the aquifer sample is without bias. That is, the sample comes from nearly the entire aquifer and not just a small part of it.
GEOHYDROLOGIC SETTING
The Tucson ground-water basin is located in the Basin and Range Physiographic Province of the arid American southwest. This area is characterized by infrequent but sometimes violent local thunderstorms in the summer and widespread frontal storms in the winter. Recharge to the ground-water-flow system is primarily by infiltration of runoff in the various stream channels throughout the area. The stream channels generally flow only after rainfall events. Average yearly precipitation range from 10 to 12 inches (254 to 305 mm).
The aquifer is comprised of Tertiary to Quaternary alluvium that occupies down-faulted blocks between the surrounding mountains.
Ground water is usually under unconfined conditions. The direction of ground-water flow is generally from south to north. In some areas the alluvium may be as much as 7,000 feet (2,134 m) thick (Davis, 1965). The alluvium ranges from fine-grained silt and clay through poorly- to well-sorted sand to poorly- to well-sorted gravel.
ELECTRIC ANALOG MODEL
An electric analog model study of the Tucson Basin aquifer was conducted by Anderson (1970). His model included an area of about 750 square miles and was constructed with a nodal spacing of one-half mile (0.8 km).
DIGITAL MODEL
A digital model of the Tucson Basin was developed by Supkow using the same nodal spacing as the electric analog model and covering approximately the same area. The digital model has a total of 2,497 nodes each covering an area of 1/4 square mile (0.65 km2).
Supkow used calibration process and adjusted aquifer-transmissivity values at individual nodes by trial and error until calculated water-level changes matched historical water-level changes. He stopped the calibration process when the average nodal error (the difference between calculated and historical water-level changes over the 19 year period from 1947 to 1966) for the entire model was reduced to 5.65 feet (1.72 m).
Supkow prepared an aquifer-transmissivity isopleth map of the Tucson Basin as determined by the digital modeling process. In some parts of the aquifer the transmissivities are somewhat less than they were prior to the present period of heavy pumping that caused a decrease in saturated thickness.
THEORY OF TRANSMISSIVITY DISTRIBUTION IN AN ALLUVIAL AQUIFER
The alluvial sediments within the Tucson aquifer were deposited on some sort of pre-existing erosional surface. We can expect that this erosional surface, prior to being covered by alluvium, had some sort of drainage network. If we assume that Horton's Laws of stream orders were as valid in the past as they are at present, we can expect that they applied to the drainage network of the paleo-erosional surface.
Horton's Law states that there is an exponential relationship between stream order and drainage network parameters such as area of drainage basin and length of stream. Stream order is a measure of the hierarchy of stream tributaries in which (for a given map scale) the smallest stream is assigned the lowest order of "1" and the larger streams are assigned succeedingly higher orders.
For example, a first-order stream has no tributaries. A second-order stream has only first-order streams as tributaries. A third-order stream has only first- and second-order streams as tributaries and so on. If we prepare a semi-logarithmic plot of stream order versus length of stream or area drained for any catchment area in the world, we obtain a straight line where the highest order stream has the longest length and drains the largest area. The lowest-order streams have the shortest length and drain the smallest areas. Likewise, a semi-logarithmic plot of stream order versus number of streams is also a straight line. The first-order streams for any particular drainage net are most numerous.
In consideration of the above relationships, Supkow hypothesized that there should be an exponential relationship between transmissivity of an alluvial aquifer and the area of the aquifer having the specified transmissivity. We would expect the alluvial aquifer to have more low-valued transmissivities than high-valued transmissivities. In terms of a probability density function (PDF) this would be
f(T) = 1/l e -T/l for T>O
f(T) = 0 otherwise
where
T = transmissivity
l = arithmetic mean value of transmissivity.This PDF refers only to the frequency distribution of transmissivity and not to the locations of any particular transmissivity in space.
TEST OF HYPOTHESIS
To test this hypothesis, a statistical study was made of the transmissivity values used in the digital model of the Tucson Basin aquifer. Values of aquifer transmissivity ranged from <1,000 gallons per day per foot (<124 m2/d) to as high as 450,000 gpd/ft (5,580 m2/d). The arithmetic mean of all 2,497 transmissivity values in the model was 54,848 gpd/ft (680 m2/d).
The probability P that T should lie between specified limits T1 and T2, is given by:
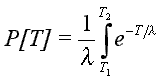
A plot of probability versus transmissivity with l = 54,848 gpd/ft (705 m2d) is given by the solid curved line in the Figure 1. For example, the probability of transmissivity values less than or equal to 10,000 gpd/ft (<=124 m2/d) is 0.1667, the probability of transmissivity values less than or equal to 50,000 gpd/ft (<=620 m2/d) is 0.5981, and the probability of transmissivity values less than or equal to 450,600 gpd/ft (<=5,587 m2/d) is 0.9997. This means that chance of successfully drilling randomly to find areas of the aquifer with transmissivity greater than 450,000 (5,580 m2/d) is practically nil.
A plot of probability versus transmissivity with l = 54,848 gpd/ft (705 m2d) is given by the solid curved line in the Figure 1. For example, the probability of transmissivity values less than or equal to 10,000 gpd/ft (<=124 m2/d) is 0.1667, the probability of transmissivity values less than or equal to 50,000 gpd/ft (<=620 m2/d) is 0.5981, and the probability of transmissivity values less than or equal to 450,600 gpd/ft (<=5,587 m2/d) is 0.9997. This means that chance of successfully drilling randomly to find areas of the aquifer with transmissivity greater than 450,000 (5,580 m2/d) is practically nil.
The plotted points represent probabilities of transmissivity as determined by actual count of the number of nodes in the digital model having transmissivity values less than or equal to the plotted transmissivity value. We can see that there is a reasonably close fit between the calculated curve and the observed data points. The data points used to plot Figure 1 are in Table 1.
DISCUSSION OF RESULTS
It is common knowledge that alluvial basins consisting of coalesced alluvial fans have the coarsest, most-poorly sorted detritus around the periphery of the basins. Because of the poorly-sorted detritus and the thinner saturated thickness around a basin periphery, the transmissivity there is generally lower. Although transmissivity, (the product of permeability and saturated thickness), is a derived mathematical parameter, it is a parameter that has real meaning in the real world of alluvial aquifers. It is a quantity that results from the various inputs that form a dynamic alluvial aquifer system.
Given the present aquifer, an increase in average annual rainfall will increase the average recharge rate. This will result in more ground water flowing through the system. Under similar hydraulic gradients and greater saturated thickness, the aquifer will have higher transmissivity. Conversely, a decrease in the quantity of ground water flowing through the aquifer will result in lower aquifer transmissivities.
It thus appears that the average value of transmissivity for an alluvial basin aquifer given by "l" is a function of the climate and the drainage area of the basin. If is true, it then might be possible to predict the mean value of transmissivity within an alluvial basin if we have the climatic data and the area of the rainfall catchment for the basin, even though no information is available on the thickness or permeability of the sediments. In following this reasoning, if we find another ground-water basin similar in size and climatic conditions to the Tucson Basin, we would expect that basin to have an average transmissivity similar to that of the Tucson Basin.
Now that more and more aquifer systems are being modeled by means of digital computers, analyses such as the one described here could be carried out routinely. It would be a simple matter to check on the validity of the relationships postulated herein.
Certainly, the a priori knowledge that the transmissivity must be exponentially distributed would be a powerful constraint on construction of the model.
REFERENCES
Anderson, T. W., Electrical-analog analysis of the hydrologic system in Tucson basin,
Arizona: U.S. Geol. Survey Water-Supply Paper 1939-C, p. 15-24, 1970.Davis, R. W., A geophysical investigation of hydrologic boundaries in the Tucson
basin, Pima County, Arizona: unpublished Ph.D. dissertation, University of
Arizona, 64 p., 1965.Gates, J. S, Worth of data used in digital-computer models of groundwater basins:
unpublished Ph.D. dissertation, University of Arizona, 214 p., 1972.Supkow, D.J., 1973, Transmissivity Distribution in the Tucson Basin Aquifer,
Proceedings of the Arizona Section of the American Water Resources Association
and the Hydrology Section of the Arizona Academy of Science, May 5-6, 1973,
Prescott, Arizona, PP. 113-123.
© 1999 AGW Consultants. All Rights Reserved.